
大人でもn進法と言われて「うん???」となる方もいるでしょう。
ふだんの生活で馴染みがないように見えますが、実はそうでもないのです。
今回は、身近な例を挙げてn進法の仕組みを説明します。
理解を確実にするため、例題を一緒に解いていきますので安心してお読みください。
馴染みのない「n進法」ですが数字の奥深さに気づけます。ぜひ最後までお読みください。
意外と身近な「n進法」
n進法と聞けば難しく感じますが、身近なものでn進法が使われているのに気づけば「他にもあるの?」と探したくなります。
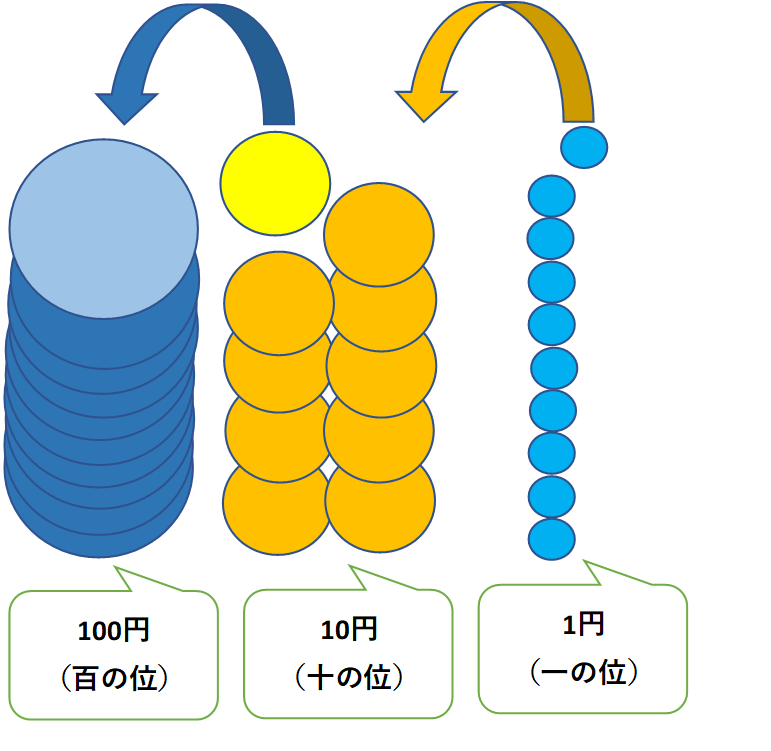
例えばお金。1円から始まり2、3…1円玉十枚で10円玉。10円玉が10個で100円玉。100円玉10個で千円札。
この仕組みにn進法が隠されています。
お金のように、1円10枚で新たな硬貨「10円玉」になる数字の進み方を10進法といいます。
「10のかたまり」で進む、これを覚えてください。
次に時間で探してみましょう。1秒が60個分で60秒=1分となります。
1分が60個分=1時間のように、時間は「60のかたまり」で進みます。つまり60進法です。
同じ”時間”でも週ではどうでしょう。
7日で1週間、14日で2週間と「7のかたまり」で進むから7進法、月は28~31日のまばらですから、少し飛ばします。
年でいえば12か月で1年、24か月で2年と「12のかたまり」で進むから12進法です。
ちなみにコンピューターの制御には0と1のみを使うので2進法となります。
このように、意外と身近に「n進法」があるのが分かりますね。
10進法の仕組みを復習しよう
この章では馴染みのある10進法を解説します。
その決まりが理解できれば、10以外の数字でも仕組みの説明ができます。
おもちゃのお金でいいのでその感覚をつかみます。
ない場合は手書きでも構いません。感覚をつかめるように工夫しましょう。
まず何もない状態0を意識。
0からスタートし1、2、3…とならべ9まで並べます。
10個めで”かたまり”が生まれました!それを袋にいれます。
「10の袋」の出来上がり。
同じように1円玉10個入りの袋を作り「10の袋」を10個分。
そして新たな”かたまり”の誕生です。それを大きめの袋にいれます。
「10が10個で100の袋」の出来上がり。
続いて…と進めれば、”かたまり”が進法の重要な要素になるのが分かるでしょう。
お金の場合、10の”かたまり”だから10進法となります。
「あ、10進法の10は”かたまり”の意味だ!」と気づきます。
ついでに位取りの復習もできます。
つまり先ほどの1円は一の位。「1」円だからです。
「10の袋」の場所は十の位、「100の袋」の場所は百の位と連動します。
この考え方をもとに次章で2進法の練習をしましょう。
2進法の仕組みを理解しよう
2進法は0と1のみの仕組み。
先ほどの10進法で使う数からすれば「えっ、これだけ?!簡単!」と思うのは当然でしょう。
初めの位はやはり「1」なので一の位。
2進法では次の2で「2のかたまり」が生まれます!
「えっ、もうかたまり?!」と驚くでしょう。
先ほどと同じように”かたまり”である「2の袋」を作ってみます。
また、0、1→「2の袋」を作ります。
そのままだと永遠に「2の袋」を作り続けるので一旦とめます。
つまり「2の袋」が二つある時点で立ち止まり「この位は何の位?」と質問してください。
10進法のときは「10の袋」の場所は「十の位」でした。
2進法はどうでしょう。「2の袋」の場所をいったい何の位といえばいいのでしょうか?
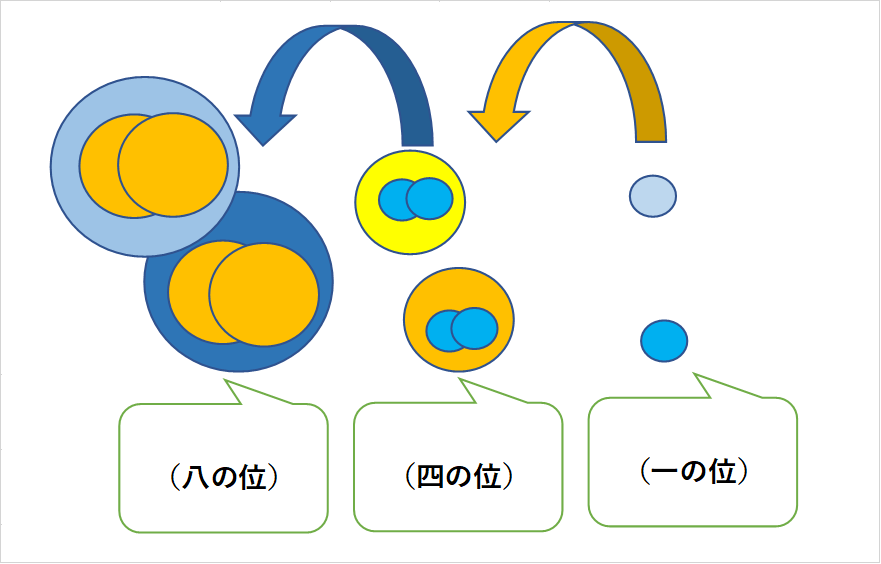
「2の袋」が二つあるから2×2で「四の位」となるのです。
10進法が1が10個で10、10が10個で100、100が10個で1000となっていたように、
2進法の場合は1が2個で2、2が2個で4、4が2個で8、8が2個で16…となっていくのです。
つまり2進法の位取りは「一の位」「二の位」「四の位」「八の位」「十六の位」となります。
n進法の仕組みを理解しよう
これが理解できると他の数字で応用できます。
例えば3進法なら1(一の位)、1が3個で3(三の位)、3が3個で9(九の位)、9が3個で27(二十七の位)…。
5進法なら1(一の位)1が5個で5(五の位)、5が5個で25(二十五の位)、25が5個で125(百二十五の位)…
となります。
「10より数字が小さいのに計算がめんどうだ……でもかけ算を使えばすぐできる」
という感想がもれるかもしれません。その気づきが大切です!
ルールがあると分かれば、簡単に求める方法を探そうとします。
最初から方法や公式を教えても思考力は育ちません。
「n進法」も同様。nの文字(記号)を用いれば大きな数の位取りも簡単です。
つまりn進法の位は「一の位→nの位→n×nの位→n×n×nの位」と表せます。
nを使って表せるとなれば簡単に計算ができるでしょう。
実際にn進法の問題を解こう
10進法の123を式で表すとどうなりますか?
100が1個と10が2個と1が3個集まった数字が123ですから、100×1+10×2+1×3=123となります。
これをもとに次の問題を解いてみましょう。
n進法→10進法にする問題
では、123の数字が3進法だとしたらどうなりますか?言い換えれば「10進法にすると?」となります。
前の章で求めたnの位取り「一の位→nの位→n×nの位→n×n×nの位」と使いましょう。
今回は3けたですから→並び変えると「n×nの位、nの位、 一の位」の順です。
3進法は「3×3=九の位、3×1=三の位、一の位」。
つまり、123のそれぞれの数字を位に当てはめます。
9×1+3×2+1×3=18。
つまり、3進法の123は10進法の18となるのです。
では、123を4進法と考えた場合どうでしょう。
同じように「n×nの位、nの位、 一の位」ですから
それぞれ「4×4=十六の位、4×1=四の位、一の位」となりますね。
よって16×1+4×2+1×4=28。
つまり、4進法の123は10進法の28となります。
各けたの位には、ある一定のかたまりが存在しているので、けた数をかければいいのです。
ただ、数字が小さければ小さいほど混乱してしまうかもしれません。
その場合、先ほどの10進法を使った求め方に戻りましょう。
10をnに変える考え方を確認すると混乱を防げます。
10進法→N進法にする問題
まず、時間で使う60進法で練習します。
使い慣れている位取りの方で説明した方が、仕組みが分かりやすいからです。
とはいえ、例えばこのような問題です。
「8765秒を60進法で表しなさい」
聞き慣れない時間表現ですね。これを60進法に直しましょう。
まず8765秒を60で割ります。
これで〇分の単位が生まれます。
再び60で割れば今度は〇時間の単位が見えてきます。
やってみましょう。
146÷60=2あまり26(2時間と26分)
8765秒を60進法で表すと「2時間26分5秒」(これが答え)
これが10進法をn進法にする方法です。
では、432を5進法で表すとどうなるでしょう?
時計の問題と同じように計算します。5進法ですから、わる数は5ですね。
86÷5=17あまり1
「あれ?まだ5でわれる…」
17÷5=3あまり2
つまり…
困ってしまいました!
時間の場合は「〇時間〇分〇秒」とすっきりしたのに、どうしたらいいでしょうか。
この場合も先ほどの60進法を参考に考えます。太字を見てください。
146÷60=2あまり26(2時間と26分)
8765秒を60進法で表すと「2時間26分5秒」
最終的にに出された2(時間)が一番大きな位の数字。
その後は順に26、5というように、余りの数字が続きます。
つまり「2時間26分5秒」ですね。
5進法に戻し、同じように太字にしました。
432÷5=86あまり2
86÷5=17あまり1
17÷5=3あまり2
つまり、最後に出された答え(解)3が一番大きな位の数字で、
続いて2、1、2となり、よって432を5進法にすると3212となるのです。
これを逆さ筆算にすると次のようになります。
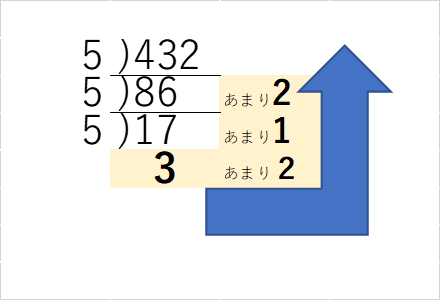
下からL字を書くように読み取ればすぐ解けるでしょう。
始めから「逆さ筆算」を教える場合もありますが、60進法の考え方から順序立てて「逆さ筆算」に導くと理解が深まります。
まとめ:n進法を解くヒントは身近にあり!
いかがでしたか?n進法という言葉を聞いただけで「何だか難しそう」と思う場合、身近な例を参考にすると意外と親しみやすくなります。
位取りの仕組みが分かれば、nと表す理由やよさも分かってきます。
そしてn進法から10進法に変えたり、10進法からn進法にしたりする方法も簡単になるでしょう。
もしつまづいたとしても、10進法や60進法のように馴染みのある位取りに戻れば記憶と思考を呼び戻せます。
ぜひ、この記事を参考にご家庭でも練習してみてください。