
分配算とは、ものを配るときにどのように分けたかを求める問題です。
「和と差」だけで問題が解ける和差算と異なり、分配算の特徴は「比」の考え方が使われている点です。
「和と差」と「比」という情報を基に、どのようにものが分けられたかを解く分配算。
実際に練習問題を使って確かめましょう。
分配算に苦手意識があり線分図のかき方・使い方が分からない場合もだいじょうぶです。
基礎から丁寧にお伝えします!解答のコツがつかめますので、ぜひ一緒に解いていきましょう。
分配算で使える線分図のかき方・考え方(基本編)
実は分配算では、特に公式を覚える必要はありません。
問題の意味「何を求めるのか」を理解し「分からない部分を順に明らかにする」思考が試されます。
実は似たような仕組みがあるため、それが分かると問題を解くのが楽しくなるでしょう。
まず、次の問題を解いていきます。
分配算では比の考え方を使う
導入でお伝えしたように、分配算の特徴は、単なる和差でなく比の考え方が入っています。
次の問題で確かめましょう。
48と2の数字とにらめっこしても見えてこない数字の世界。
少しずつひも解きましょう。この場合、まず比を取り入れます。
リンゴ ミカン
〇個 △個
2 : 1
見てのとおり、全体の数は比でいえば「2 + 1=3」となります。実際の3は48個という意味。
だから「比の値1」を求めるには、48÷3と考えます。
計算すれば16(個)となりミカンの数は16個。
ミカンが16(個)だから、16×2でリンゴの数を出せます。
16×2で32個。リンゴは32個です。
いかがでしょうか?たしかめ算でリンゴ+ミカン→32 + 16で48個ですから、合っていますね。
1つめのリンゴとミカンの問題では線分図を使いませんでした。
しかし、複雑な問題になると比が見えにくい場合があります。
このとき比が分からなくても、線分図をかけば見えてきます。
「比が分からない場合はまず線分図!」と考えて間違いはありません。
次の章で早速、線分図が登場します。続けて一緒に解いていきましょう。
分配算で線分図を使う(その1)
比の考え方を取り入れるのが分配算ですが、その過程に和差算が入る場合があります。
次の問題で解説します。まずはやってみましょう。
3倍の3、合計の164個の164は、先ほどと同じ種類の数字です。
4はどうでしょう。そうです。ここで「比」以外の数字が入りました。
”〇個多い”という和算に関する数字です。
少し難しいですね。線分図でかいてみましょう。
「比」に着目しますから、かならず大きさをそろえてかくこと。これは重要です!
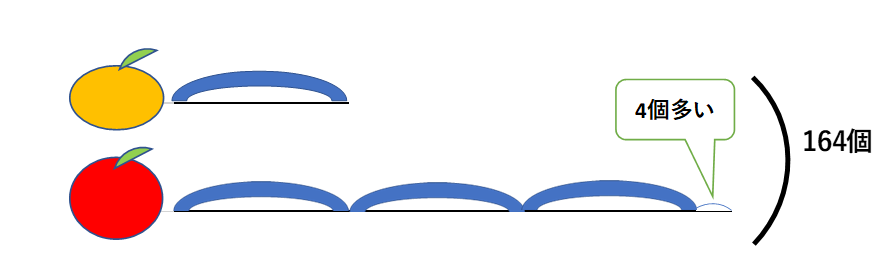
先ほどの問題は「多い・少ない」がありませんでした。
しかし、この問題は比の値1を求めるのに、まず余分な(半端な)数字を取る→引く必要があります。
つまり4(個)をひくのです。
そこで、164ー4を計算すると160。
次に160÷4で40となり比の値1は40(個)と分かります。
比の値1=ミカンの数ですから、ミカンが40個、リンゴが40×3=120個となりますね。
いかがですか?「比」が分かれば解きやすくなります。
そして「比」を分かるようにするのは「線分図」。
なぜなら線分図でイメージがはっきりするからです。
分配算の問題は、より複雑になると言葉や文字だけで導くのは難しい場合があります。
順序立てて考えを整理するためには、線分図のかき方に慣れていた方が”お得”です!
分配算で線分図を使う(その1)
次の問題に挑戦しましょう。
もっとも異なる点はどこでしょう。
そうです「〇個少ない」点です。先ほどは”余分”だったので引きました。
今後は”足りない”ので足します。きっかり4(倍)にする必要があるからです。
線分図は次のようになりました。

まず、全体の数の98(個)+2をします。100個になりました。
これを比の値1を求める計算に戻します。
つまり100÷(比の合計1 + 4)=20となり、ミカンの数が20(個)、リンゴの数が20×4-2となり78(個)となります。
いかがですか?ますます得意になりそうですね。
では次の章で、他の種類に挑戦しましょう。
分配算で使える線分図のかき方・考え方(応用編)
3種類の分配算に挑戦!
これまでは2種類のものを比べてきました。
今度は3種類!ただ、やり方は変わりません。
線分図、和差算、比の三本柱で考えながら、次の問題を解いてみましょう。
まず基準を何にするのか決めます。この場合ミカンを基準にすると考えやすいでしょう。
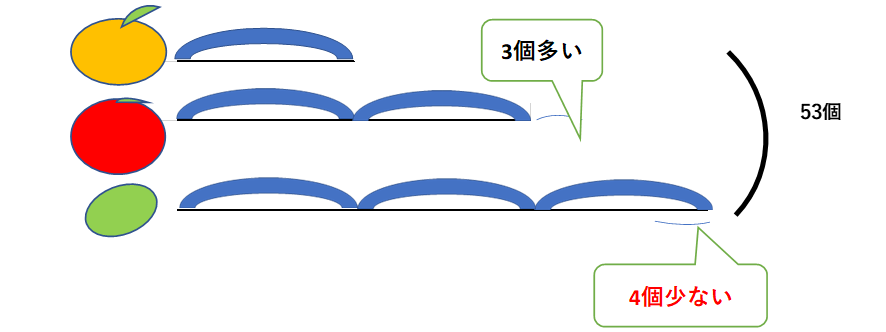
全体からまず和差算で調整します。これが、2種類の場合と同じです。
つまり全体の数から余分な3を引いて足りない4を足すのです。
53-3 + 4=54になりますね。線分図を使えば、比の部分も見えてきます!
・・・・・・・・・・・
ここで補足!
線分図よりも方程式の考え方で求めた方が頭の中が整理しやすい子もいます。
その場合は次のようになります(ただし立式する場合も線分図のかき方を覚えておいた方が考え方を整理しやすいです)。
●ミカンをXとすれば、X、X×2 + 3、X×3ー4の合計が53。
●立式すると「X+(X×2+3)+(X×3ー4)=53」
※中学生になると6X-1=53という計算式が間に入りますが、得意な子は使ってもいいでしょう。
・・・・・・・・・・・
ここからは線分図から見える考え方と同じです。
53ー3+4=54
54÷(比:1+2+3)=9
よってミカンは9(個)、リンゴは21(個)、キウイは23(個)となります。
線分図を使うと(比:1 + 2 + 3)が見えるので便利ですね。
※終わりに全体の53個になるか確かめましょう。
全体の数が分からない?!
今までは全体の数が分かっている問題でした。今度は全体の数が分からない場合を考えましょう。
全体の数が分からないうえ、3種類の数が混合しています。
難しい問題ですよね。ただし、今までの方法を使えばできます。
まず、線分図をかいてみましょう。
文章に2倍、3倍のように「比」が入っていますから、線分図で比の実態を明らかにしましょう。
そこが大きなヒントです。
解けるところから攻めていきます。
まず文章の中の「AさんはBさんの3倍より5本多い」からいきましょう。
次のように線分図をかいてみます。
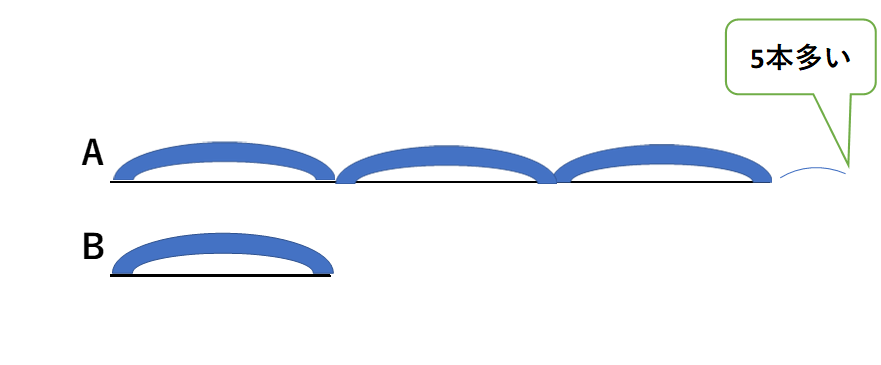
次に「CさんはBさんの2倍より2本少ない」の部分を線分図に加えます。
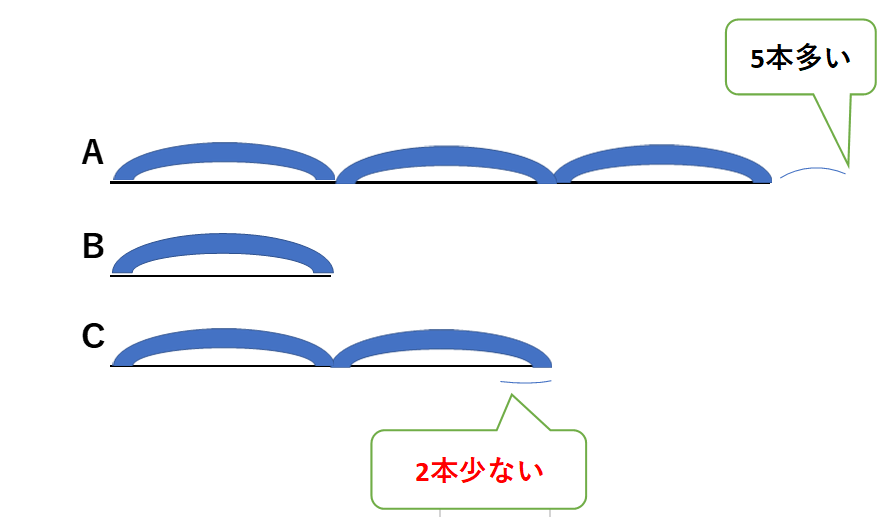
さらに「AさんとBさんの差が17本」ですから、次のようになります。
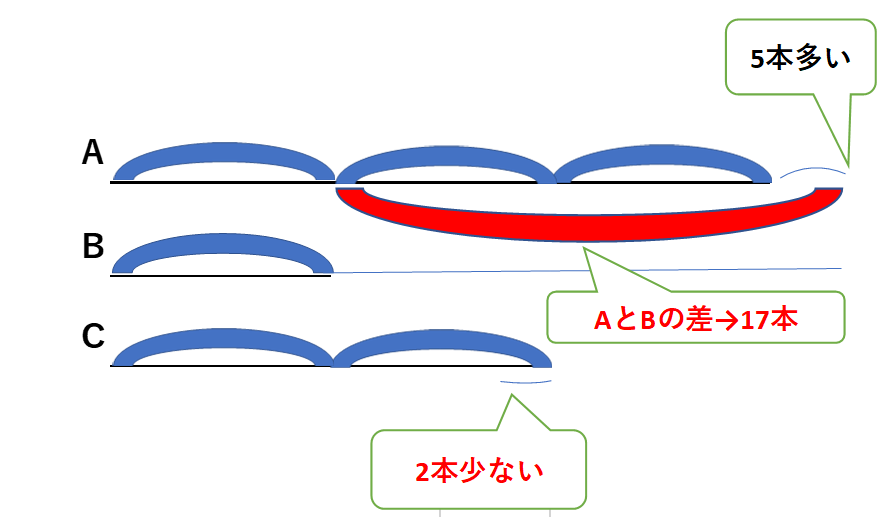
「かいたはいいけど、いったいどこから求めればいいの?」と思うかもしれません。
が、このとき「比の値1」をどう求めるか?がポイントになります。
線分図を見てわかるように赤の部分に気づけば17-5から「比の値の2個分…17-5=12」を発見できます!
つまり12÷2で6。比の値1が6と分かりますね。この値はそのまま、Bさんの数になります。
さらにCさんの数はBさんの2倍より2本少ないわけですから6×2-2で10本。
Aさんは6×3 + 5で23本ですね。よって合計は23 + 6 + 10で39本となります。
線分図をかいても分からない場合は?!
線分図をかいてもなかなか答えを導き出せない場合もあるでしょう。
線分図をかくとき「比の値1」の大きさがまちまちであったり「少ない・多い」のあたりがごちゃごちゃになったりすると分かりにくいです。
この記事を参考に、似た問題で線分図のかき方を練習しましょう。
ただ、複雑になると線分図をかいたとしても、どこから手をつければよいか分からない場合もあります。
そのときは「比の値1を見つける!」に徹しましょう。
そもそも線分図はそのためにあります。
算数の楽しさや多角的に見る・考える力をつけられるのも分配算のメリットです。
「謎解きのように探したり考えたりするのが楽しい!」と思えたら算数を好きになるでしょう。
まとめ
今回は分配算の解き方について、線分図や比の仕組みに着目しつつ解説しました。
順番は次のようになります。
「文章の意味を理解する」→「意味を整理しながら線分図をかく」→「線分図から比の値1を探す手立てを考える(和差もときに必要)」→「わり算で比の値1を出す」→「比の値1と和差などを使って個数求める」
こうすれば、求められる数値を導き出せます。
基本問題から線分図のかき方・考え方を習得しましょう。
少しずつ難しい問題に挑戦し自力で解けるようになれば自信もつきます。