
中学校以降の数学でも「等差数列」は使われますが、苦手な子はいます。
小学校低学年から数の規則性を見つけるのを「楽しい」と思えればいいのですが、そう簡単にいきません。
「公式を覚えればよし」で実際上手くいったとしても、そこに落とし穴があります。
本来学ぶべき「考え方」が抜け落ち、応用問題でつまづいてしまう恐れがあるのです。
今回の「等差数列」では、単に「公式」を提示するのではなく、そこに至るプロセスを説明します。
等差数列の仕組みをしっかり理解し、万が一公式を忘れてしまっても対処できる基礎力を身につけましょう。
「等差数列」とは?
等差数列とは、言葉どおり「等しい差で変化する数の列」となります。
次の数列を使って説確かめましょう。

このように、等差数列は「はじめの数」からスタートして「等しい差」で順に増えていく数の並びをさします。
「等しい差」を一般的に「公差」といいます。
それでは次に、・・・と続くN番目の数を求めていきます。
その規則性が分かれば、一つめの公式を導き出せます。
「等差数列」の公式とは?
この章では「等差数列」のさまざまな公式を取り上げます。
まずN番目の数を求める問題から始めましょう。
N番目の数を求める公式とは?
先ほどの数列をもう一度出します。

「はじめの数」は2です。
それに2 + 3で5、5 + 3で8、8 + 3で11のように数字が変わっていきますね。
3つずつ足されていくので「公差」は3となります。
「じゃ、何が変わるの?」といえば、N番目の数が変わっていくのです。
たとえば2番目の数は(2 + 3で)5、3番目の数は(5+3で)8、N=4番目の数は(8 + 3で)11のように変わりますね。
ここで、着目するのは3に関連する数字です。もう少し解説を加えます。
1番めの数は「はじめの数」ですから2は決まり!
ただN番目をN=2としたときは、どうでしょう。
5はどのように求められるかといえば「はじめの数2」に「公差3」を足しますね。
この3は公差の3が1つという意味で(3×1)となります。
整理すると「2+(3×1)」で5という「2番目の数」が生まれるのです。
N=3としたときはどうでしょう。
8はどのように求められるかといえば「はじめの数2」に「公差3」を2つ分つまり(3×2)を足します。
整理すると「2+(3×2)」で8という「3番目の数」が生まれます。
N=4としたときは?
11は「はじめの数2」+(公差3×3つ分)つまり「2+(3×3)」で11という「4番目の数」が生まれます。
赤字をご覧ください。
N‐1になっているのがお分かりでしょう。
つまりN-1が公差のいくつ分(公差の個数)になっているのです。
このように実際の数字を当てはめながら、規則性を見つけます。
考え方のルールや規則が分かれば「公式」を導き出せるのです。
今回は「等差数列」の規則性・公式が分かりました。
それでは、「等差数列」のほかの公式について、練習問題で確かめましょう。
「等差数列」のほかの公式も確認しよう
Q1:
等差数列:3、5、7、9…の30番目の数を求めましょう。
先ほどの公式に当てはめて求めます。
「はじめの数」は3「公差」は2。
そしてNは30となりますから、3 + 2×(30‐1)で61となります。簡単にできました!
では次の問題はどうでしょう。
Q2:
81は数列3、5、7、9の何番目の数ですか?
今度は何番目?と聞かれています。
つまりN番目。図で表すと次のようになります。

「はじめの数」の3は変わりません。
「公差2がいくつあるのか?」これが分かれば80にたどり着きます。
つまり、公差×(N-1)を求めるのです。
それにはまず、81から「はじめの数3」を引く必要があるでしょう。
81-3=78。
その78は公差2の(N‐1)個分ですから、78÷2で39。
N-1=39ですからN=40となります。
この考え方で、N番目の数を求める公式を導き出せば次のようになります。
Q3:
上の問題で「公差」が分からず40番目が81と分かっている場合はどうでしょう。
81‐3=78を出すまでは同じです。
公差の個数はN-1ですから40‐1=39。
よって78÷39で公差の2が求められます。
公差を求める公式は次のようになります。
最後にもう一つ。
「はじめの数」が分からない場合はどうでしょう。
たとえば、次の問題です。
Q4:
15番目の数が123で公差が8の場合、はじめの数はいくつですか?

つまり公差(8)の個数も15番目の数字123が分かれば分かりますね。
8×(15‐1)で112です。
つまり「はじめの数」は123から112を引いた数字、11と分かります。
これを公式に表すと
いかがでしょうか。
ただ「公式をいくつも覚えるのもなんだかな〜」とやる気が失せてしまいそうです。
その対策を次の章でご紹介します。
4つの公式を覚えなくても1つあれば解ける?!
まず、4種類の公式を整理しておきましょう。
N=【(N番目の数-はじめの数)÷公差】+1
公差=(N番目の数-はじめの数)÷(Nー1)
はじめの数=N番目の数‐【公差×(Nー1)】
この公式をそのまま覚えて問題を解く子もいるでしょう。
しかし、忘れてしまった場合は困ります。
そうならないようにするには?
やはり「等差数列」の規則性をしっかり確認する必要があります。
そのうえで、覚えやすい公式を1つ覚えて応用する子もいるでしょう。
覚えるなら4つより1つの方が時間も労力もかかりません。
先ほどの「15番目の数が123で公差が8の場合、はじめの数はいくつですか?」の問題で解説します。
はじめの数=N番目の数ー【公差×(N‐1)】を使わずに、はじめの数+【公差×(N‐1)】=N番目の数の公式を使います。
つまり「はじめの数」を▢か✕にして解くのです。
赤字の公式に当てはめるとX+【8×(15‐1)】=123となりますね。次の考え方を確かめましょう。
X+【8×(15‐1)】=123
X+8×14=123
X+112=123
X=123‐112
X=11
このように不明な文字Xを含む式を=で結んだものを方程式といいます。
中学1年生ではまず、方程式を学習します。
=の左側を左辺、右側を右辺とよびます。
等差数列の公差が分からなかった場合として次の方程式を解いてみましょう(公差=X)。
※はじめの数が3で14番目の数が159の場合の公差を求める場合。
3+X×(14‐1)=159
3+X×13=159
3+X×13‐3=159‐3
X×13=156
X×13÷13=156÷13
x=12
「式が長い!」と思った方もいることでしょう。
ルール「等式の性質」を使っているのです。
実際は、赤の太字部分(左辺)を省く場合が多いのですが。
⑴ A+C=B+C 両辺にそれぞれ同じ数を足しても等式は成立。
⑵ A-C=B-C 両辺にそれぞれ同じ数を引いても等式は成立。
⑶ A × C=B× C 両辺にそれぞれ同じ数をかけても等式は成立。
⑷ A ÷ C=B÷ C 両辺にそれぞれ同じ数をわっても等式は成立。
先ほどの方程式を解くプロセスでの赤字の部分が「等式の性質」を使ったもの。
同じ数を足したり引いたりかけたりわったりすれば消えてなくなる→すっきりと計算できる、というわけです。
難しく感じる場合は無理しない方がいいでしょう。
ただ、慣れると中学入学後のスタートがスムーズにいきます。
いずれにしても単に「公式を覚えればいい」と思うのはおすすめできません。
数列の仕組みや考え方がしっかり理解できて「公式を利用する」のはいいのですが、それらが分からずに覚えるのは、つまづきの原因になります。
数列の仕組みが分からないうちは、簡単な問題で何度も練習し「考え方」に慣れるようにしましょう。
【応用編】等差数列の和とは?
この章では、等差数列の応用編として「N番目までの和」の求め方を解説します。
たとえば次のような問題。
Q5:
1、4、7、10、13、16…このような数列の1番目から10番目までの和を求めなさい。
1 + 4 + 7 + 10 + 13 + 16...と順番に計算するのは大変で間違えやすいですが、一応やってみましょう!
公差が3と分かりますから10まではこうなります
1、4,7,10、13、16、19、22、25、28
1 + 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28=計算すると145となりました。
しかしこのあと20番目となったらさらに時間がかかります。
そのために「公式」を見つけたいですね。
次の図をご覧ください。
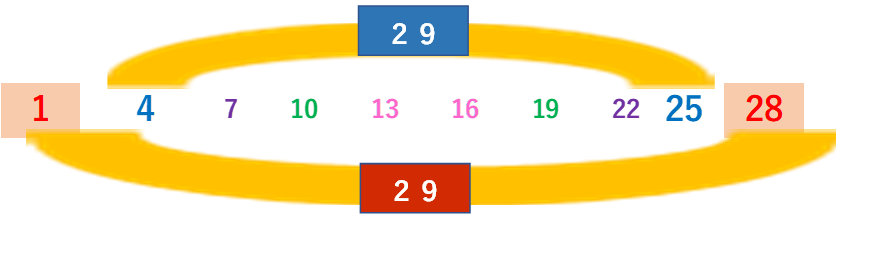
10個の数列の「はじめの数」と「おわりの数」を足せば29。
「2番目の数」と「最後から2番目の数」を足すと29になります。
ほかの数も同様に7と22のセットで29、10と19のセットで29、13と16のセットで29。
つまり29のセットがぜんぶで5つあることがお分かりでしょう。
ただ、この5は数字が10個の場合に限ります。
20個であれば10個、100であれば50個になるのです。
すなわち10÷2をすればセットが何個あるかが分かります。
今回のように「はじめの数=1」「公差ー3」「10番目の数が28」すべてそろっている中での規則性を探せば、等差数列の和をもとめる公式は次のようになります。
※「おわりの数」=N番目の数
生まれた公式で先ほどの等差数列の和を確かめましょう。
(1+28)×(10÷2)で145となりました。
実際の計算と合っていますね。
ところで、今回は1から始まる公差3、10番目までの数列の和でしたが、100番目となったらどうでしょう。
実際書き出して確かめるには、大変になります。
まず100番目の数を求めなくてはなりません。
そこで、一番初めの「等差数列」の公式を引っ張ってきます。
つまりN番目の数=はじめの数+【公差×(N-1)】。
100番目ですから1 + 3×(100‐1)→1 + 3×99=298となります。
100番目の数が298と分かりました!
そこで「等差数列の和」の公式に当てはめてみましょう。
(はじめの数₊おわりの数)×(N÷2)
おわりの数は100番目の298ですから、
(1+298)×(100÷2)=299×50=14950
14950となりました!
実際にすべて足していくとなると時間と労力がかかりますが、こうして求めるとすっきりしますね。
まとめ
いかがでしたか?「等差数列」の仕組みや公式につながるプロセスが理解できたら幸いです。
単に公式を覚えるのではなく、考え方が分かればたとえ公式を忘れたとしても解答できます。
「等差数列」が分からなくなったらこの記事を参考に考え方を整理しましょう。
まずは簡単な問題を何度も解いて理解を確実にする、これが鉄則です。
中学以降の数学に通じる「等差数列」。
苦手意識を少しずつ減らし「楽しさ」を感じるまで練習していきましょう。