「平均」という言葉は日常生活でよく使われます。たとえば「平均気温」。
気象庁の観測データにもとづき、1日の場合は日平均気温、1か月の場合は月平均気温と呼ばれます。
ほかに「平均寿命」「平均年収」「平均株価」などニュースやWebでも使われますね。
今回まず「平均」に関するイメージをクリアにしましょう。
単なる数字・公式に当てはめた計算としてでなく、図形(面積)のイメージで攻略します。
実際の練習問題で「平均算」の仕組みをひも解いていきましょう。
そして、応用問題でしっかり確認します。
平均算に苦手意識を持っている子にも分かるように解説しますので、ぜひ最後までお読みください。
そもそも「平均」とは何?
まず次のようなブロックを使った山があったとします。
これを平らにならす場合、あなたならどうしますか?
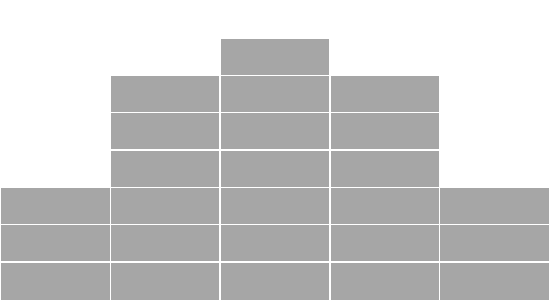
なんとなくかもしれませんが、次のようにブロックを並べ替えるでしょう。

はじめの形とおわりの形は変わりましたね。このように「でこぼこ」を「平ら」にする作業が「平均にする」という考え方です。
そして「平均算」とは、このような作業をしなくても簡単に求める計算法をさします。
「平均算」~平均を求めるための考え方と公式~
先ほどのブロックの山を使って考えていきましょう。

こちらの凸凹ブロックを砂の山とした場合、「平らにする」となれば手やスコップを使ってどうにかしますね。
あるいは棒で丁寧に均等にするかもしれません。
それはブロックを移動するのと同じ作業です。
高いところを崩せば足りない場所を埋められます。
もしもこれが、1つの柱だとしたらどうでしょう。
縮小しますが、このような柱になるはずです。

これを「ならす」としたら、ブロックの数を等しく分けようとしますね。
今回は、5列に分けたいのですから、25÷5で一列が5個となれば平らになります。
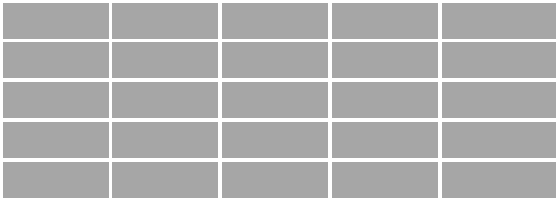
実はここに「平均算」の方法が隠されていたのです。
つまり一本の柱にしたのは「全体の数」で25(個)。
そして「列の数」は5(列)ですから、25÷5つまり”たて”に5(個)。
つまり平均は次のように求められます。
平均=全体の数÷個数
既に覚えていた「公式」ですが、今回のようにブロックで考え方をたどれば、理解が深められたのではないでしょうか。
最初にもどって先ほどの山で確認しましょう。
「もう分ったからいいよ」と思えば、先に進んで構いません。

はじめはブロックを1つずつ移動しましたが、今度はすっきりと求められます。
つまり「平均=全体の数÷個数」ですから、次のようになります。
全体の数は(左側のブロックから3+6+7+6+3)÷5=25÷5=5。
※この場合、同じ数があるので(3×2+6×2+7×1)÷5でも構いません。
いかがですか?すぐに答えが出せました!
では、次の章から実際の問題で練習してみましょう。
平均算(基礎編)
この章では、先ほどの平均の求め方を使って実際に問題を解いてみます。
全体の点数を求めてからテストの回数でわります。
つまり「全体の点数」÷「テストの回数」です。
(83+91+78+100)÷4=88 答え88点
次の問題は、少し難しくなります。一緒に解いていきましょう。
さてこの場合、全体の点数は分かりません。
分かっているのは3教科の点数と4教科分の平均が80点という点です。
先ほどの公式を思い出しましょう。
全体の数÷個数=平均でした。
分からないのは全体の数の中の「理科の点数のみ」。
それには全体の点数が分かればよさそうです。
全体の数を求めるには、平均が80点ですから80×4で求められます。
320点ですね。
ですから、320‐(75+91+85)で理科の点数が分かります。
答えは69です。いかがでしょうか。
理科の点数をXとして公式に当てはめれば
(75+91+85+X)÷4=80
(251+X)÷4=80
251+X=80×4
251+X=320
X=320ー251
X=69
このように求められます。
ただ「公式に当てはめればいい」の考え方に慣れてしまうと応用問題でつまづくかもしれません。
全体の数からいくつに分けるかの発想は、立体的に数値を捉える応用力につながります。
最初の凸凹を平らにならすイメージは忘れないようにしましょう。
平均を求める問題(応用編)
この章ではまず、文章題を取り上げます。
続いて面積で考える解き方をお伝えします。
文章問題の意味をとらえる
計算力も試される問題です。
問題の意味を正確に捉え、丁寧に計算しましょう。
公式に当てはめようとしても、何だか混乱してしまいそうです。
男子と女子とで分かれていますし、全体の点数も見えてきませんね。
しかし忘れないでください。
全体の数が分からない場合、平均と個数があれば求められます。
つまり、平均点と人数がはっきりしているのは「男子」。
そしてクラス全員の平均点が分かっていますから、合計の点数は導き出せそうです。
問題の意味を捉え、分かるところを整理しましょう。
整理したら実際に数字を出していくのがコツです。
・男子の合計点数は、平均×人数で求められます。82×12で984点。
・クラス全体の点数は同じく79 ×(12+18 )で2370点。
・つまり、ここから女子の合計点数を求められます。「全体の合計点-男子の合計点」で1386。これが女子の合計点です。
・よって1386(女子の合計点)÷18(女子の人数)で77点と出せます。
いかがですか?「問題の意味をとらえる」「分かる・分からないところを整理する」「分かるところを計算する」の作業をきちんと行いましょう。
面積の考え方を使う
考え方を求める際、面積の考え方を入れると思考力も向上します。
先ほどの問題を使って練習しましょう。
これを面積図に表すとどうなるでしょう。
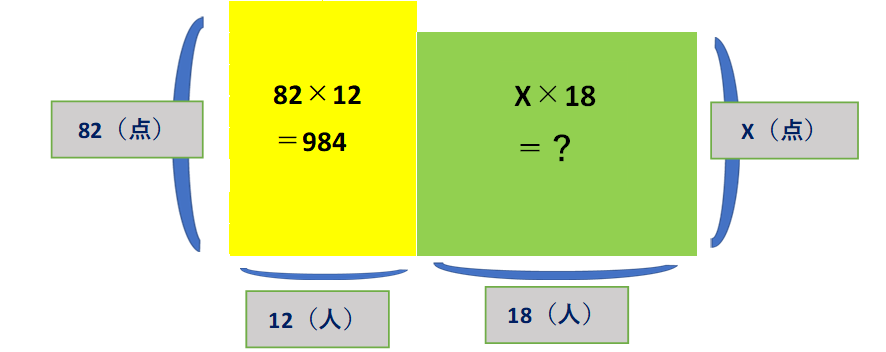
解説します。
今回は面積を求める際の「たて×横」の公式を使います。
つまり「たてを平均点」「横を人数」にしました。
”一人当たりが何点”という棒グラフがいくつも横につらなっているのをイメージしましょう。
こうしてみると全体の数を面積で求められます。
男子の場合は82×12、女子の場合はX×18です。
実は、この図形も黄色と緑の箇所が凸凹ですね(細かく言えば、それぞれ黄色と緑の中に個人の棒グラフが凸凹しているとイメージしてください)。
そこで、この黄色と緑を平らにしたのがこの長方形になりますから、両者をイコールで結んで次のように考えます。

順番に整理すれば、
・男子:82×12=984、
・全体:79×(12+18)=2370
・そして女子はX×18=?
(全体ー男子)→2370‐984=1386(女子)
・X×18=1386なので1386÷18=77
よって女子の平均点は77点となります。
まとめ:「平均算」は図形のイメージを使って攻略!
いかがでしたか?「平均算」の考え方が分かると、比較的楽しく解けます。
ただ単に公式を覚えればいい…となれば、応用問題でつまづく可能性が高いです。
平均=全体の数÷個数をたとえば「たて×横=面積」と考えれば「平均×個数=全体の数」という2次元の世界につながります。
そのイメージがもてると難しい問題を解けるようになるでしょう。
ただ、無理は禁物。まずは基本的な問題でそのイメージトレーニングをしましょう。
分からなくなった場合は、いつでもこの記事で確認してください。